DISTRIBUTIONS (mathématiques)

DISTRIBUTIONS (mathématiques)

Il est arrivé à plusieurs reprises que certaines exigences de la physique, par exemple, aient conduit les utilisateurs des mathématiques à des «calculs» non rigoureusement justifiables au moyen des concepts mathématiques existants, mais qui traduisaient avec succès la réalité expérimentale. C’est ainsi que l’ingénieur Heaviside introduisit dans l’étude des réseaux électriques (en 1894) les règles de son calcul symbolique , qui ne fut justifié mathématiquement que postérieurement. L’étude des équations aux dérivées partielles conduisait aussi naturellement à des extensions des matériaux mathématiques traditionnels; ainsi, il est normal de considérer que les deux équations:

sont équivalentes, et pourtant la première est satisfaite par toute fonction u (x ) de x seul, alors que l’expression 煉²u / 煉y 煉x n’a de sens que si u (x ) est dérivable en x . Des considérations de ce type, ainsi que l’étude du problème de Dirichlet (trouver une fonction harmonique dans un ouvert de Rⁿ connaissant ses valeurs sur la frontière) avec les méthodes de l’espace de Hilbert, ont conduit les mathématiciens à généraliser les solutions acceptables d’une telle équation en introduisant la notion de solution faible. Le mathématicien soviétique Sobolev a construit, en 1934, des classes de fonctions généralisées qui justifiaient de manière rigoureuse ce genre de considération.

La théorie des transformations de Fourier et de Laplace exigeait aussi des généralisations des fonctions. En 1926, Dirac introduisait en physique mathématique sa célèbre «fonction» 嗀⁰, nulle en dehors de l’origine et d’intégrale égale à 1, qui représentait une impulsion unité à l’instant t = 0, donc d’effet nul pour t 0. Puisque 嗀⁰ n’est pas une fonction au sens usuel (car une fonction nulle pour t 0 est d’intégrale nulle), sa justification mathématique correcte conduisait à une extension de la notion de fonction; remarquons que, dans ce cas précis, la théorie de la mesure permettait déjà de considérer 嗀⁰ comme une mesure de masse 1 concentrée à l’origine, c’est-à-dire comme un être mathématique bien défini.

Cette extension a été présentée sous sa forme actuelle par le mathématicien français L. Schwartz, dans le cadre des espaces vectoriels topologiques ; parmi ses nombreuses applications, citons: les équations aux dérivées partielles linéaires, la représentation des groupes de Lie, les processus stochastiques, les variétés différentiables, la physique mathématique, la physique expérimentale («déconvolution» et identification de systèmes).

La construction des distributions due à L. Schwartz admet de nombreuses variantes conduisant à des classes de fonctions généralisées ayant chacune un domaine privilégié d’applications: fonctions généralisées de divers types introduites par les mathématiciens soviétiques Guelfand et Šilov dans l’étude des équations aux dérivées partielles; hyperfonctions de Sato-Martineau, très utiles dans l’étude des fonctions de plusieurs variables complexes et les problèmes aux limites; fonctions généralisées de Beurling-Björk; etc.

L’exposé qui suit suppose seulement connue la notion d’espace vectoriel (cf. ALGÈBRE ou algèbre LINÉAIRE ET MULTILINÉAIRE) et la notion de suite convergente de nombres complexes (cf. nombres COMPLEXES).

1. Espaces avec notion de suite convergente

Les conditions de continuité qui interviennent dans la définition des distributions peuvent s’exprimer élémentairement en utilisant seulement la notion de suite convergente, sans qu’il soit nécessaire de préciser complètement la topologie des espaces considérés. On se propose ici de montrer comment on peut définir a priori et de manière purement formelle une telle notion sur un espace vectoriel. Les espaces vectoriels sont sur le corps R des nombres réels ou le corps C des nombres complexes.

Définition

Soit E un espace vectoriel. On dit qu’on a défini dans E une notion de suite convergente si on s’est donné un sous-ensemble 劉 de l’ensemble de toutes les suites d’éléments de E et une application de 劉 dans E qui à toute suite (x ⁿ ) de 劉 fait correspondre un élément x 捻 E, ce qu’on écrira (de manière purement formelle): (x ⁿ )x dans E, et ce qu’on lira: La suite (x ⁿ ) converge vers x ; les éléments de 劉 s’appellent suites convergentes . On impose aux données précédentes les conditions suivantes:

(a ) Pour tout élément x 捻 E, la suite constante (x , x , ..., x , ...) est convergente et converge vers x ;

(b ) Si la suite (x ⁿ ) est convergente et converge vers x , alors, pour tout nombre du corps de base R ou C, la suite ( x ⁿ ) converge vers x ;

(c ) Si (x ⁿ ) et (y ⁿ ) sont deux suites convergentes qui convergent respectivement vers x et y , alors la suite (x ⁿ + y ⁿ ) converge vers x + y .

(d ) Si (x ⁿ ) converge vers x , toute sous-suite de (x ⁿ ) converge aussi vers x .

Les conditions ci-dessus sont les propriétés des suites convergentes (au sens usuel) de nombres réels ou complexes. Comme toujours dans l’approche formelle d’une notion, on retrouve donc, sous forme d’axiomes, des propriétés vérifiées dans les situations concrètes qu’il s’agit de généraliser. Si une suite (x ⁿ ) converge vers x , on dit aussi que (x ⁿ ) a pour limite x et on écrit: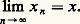

Remarquons que, pour connaître 劉, il suffit de connaître le sous-ensemble 劉⁰ de 劉 formé des suites (x ⁿ ) qui convergent vers 0 (d’après les axiomes, c’est d’ailleurs un espace vectoriel pour les opérations usuelles sur les suites). En effet, dire que (x ⁿ )x équivaut, d’après les axiomes, à dire que la suite (x ⁿ 漣 x ) tend vers 0, ce qui met en évidence que la translation de vecteur x , qui à x ⁿ fait correspondre x ⁿ + x , est une bijection de 劉⁰ sur l’ensemble 劉^x des suites qui convergent vers x . En abrégé, on dira qu’un espace vectoriel E est un e.v.s. si on a défini dans E une notion de suite convergente.

Un exemple fondamental

Il est clair que, si E est l’espace euclidien usuel de la géométrie dans l’espace, l’ensemble des suites convergentes au sens usuel satisfait aux conditions précédentes; plus généralement, si E est un espace vectoriel normé, muni d’une norme 瑩. 瑩, on peut définir directement, à partir de la norme, les suites (x ⁿ ) qui convergent vers x par la propriété suivante: La suite de nombres réels positifs 瑩x 漣 x ⁿ 瑩 tend vers 0 pour n秊; il est clair que les conditions (a ) à (d ) sont alors satisfaites. L’exemple suivant est essentiel dans la définition des distributions; on remarquera qu’on définit ici les suites convergentes sans l’intermédiaire d’une topologie.

Soit 行 un sous-ensemble ouvert de Rⁿ (c’est-à-dire que pour tout point de 行 il existe une boule de rayon 礪 0 contenue dans 行). Toutes les fonctions considérées sont supposées à valeurs complexes. Si 﨏 est une telle fonction définie et continue dans 行, on appelle support de 﨏 le plus petit ensemble fermé en dehors duquel 﨏 est nulle; 阮( 行) désignera l’ensemble des fonctions définies dans 行, admettant des dérivées partielles de tous ordres, et à support compact (c’est-à-dire borné et fermé dans Rⁿ ).

Pour désigner les dérivées partielles d’ordre quelconque, on utilise la convention des multi-indices (cf. CALCUL INFINITÉSIMAL Calcul à plusieurs variables). Par définition, un multi-indice est un système de n nombres entiers positifs ou nuls:

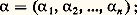on écrit alors 煉 size=1^見/ 煉x size=1^見 ou (face=F0019 煉/ 煉x ) size=1^見 pour désigner l’opérateur de dérivation partielle

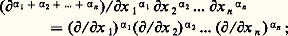cette écriture permet d’avoir, dans le cas de n variables, une écriture analogue au cas d’une variable.

Il est clair que 阮( 行) est un espace vectoriel; munissons-le d’une structure d’e.v.s. en définissant les suites convergentes. Soit ( 﨏^p ) une suite d’éléments de 阮( 行); on dira que la suite ( 﨏^p ) est convergente et converge vers une fonction 﨏 捻 阮( 行) si les deux conditions suivantes sont réalisées:

(a ) Toutes les fonctions 﨏^p , ainsi que la fonction 﨏, sont nulles en dehors d’un même compact K de 行;

(b ) Pour tout multi-indice 見, la suite des dérivées partielles (face=F0019 煉 size=1^見 﨏^p / 煉x size=1^見) converge uniformément sur K vers la dérivée partielle correspondante de 﨏:

pour p秊. Il est clair que les conditions (a ) à (d ) sont satisfaites.

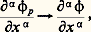Morphismes

On va maintenant définir les morphismes des e.v.s., c’est-à-dire les applications d’un tel e.v.s. dans un autre qui respectent les deux notions définissant la structure d’un e.v.s.: la structure vectorielle et les «suites convergentes».

Soit E et F, deux e.v.s. Un morphisme u de E dans F est, par définition, une application linéaire de E dans F (c’est-à-dire telle que u ( x + 猪 y ) = u (x ) + 猪 u (y ), pour x, y 捻 E et, 猪 dans le corps de base R ou C) qui transforme toute suite convergente de E en une suite convergente de F: si (x ⁿ )x dans E, alors (u (x ⁿ ))u (x ) dans F; on dit aussi que u est une application linéaire séquentiellement continue (ou «continue pour les suites»). Pour qu’une application linéaire de E dans F soit un morphisme, il faut et il suffit qu’elle transforme toute suite convergente vers 0 dans E en une suite convergente vers 0 dans F.

Voici deux exemples de morphismes de l’e.v.s. 阮( 行) dans lui-même. Si on désigne par 煉/ 煉x ⁱ l’opérateur de dérivation partielle par rapport à la i -ième coordonnée dans Rⁿ , l’application 﨏 料 煉 﨏/ 煉x ⁱ est un morphisme de 阮( 行). De même, si f est une fonction admettant dans 行 des dérivées partielles de tous ordres, l’opération de multiplication par f , qui s’écrit 﨏 料 f 﨏, est un morphisme de 阮( 行) dans 阮( 行).

Si E et F sont deux e.v.s., on peut munir l’espace vectoriel 硫 (E, F) des morphismes de E dans F d’une notion de suite convergente en disant qu’une suite u ⁿ de morphismes de E dans F converge vers u 捻 硫(E, F) si (u ⁿ (x ))u (x ) dans F pour tout élément x 捻 E. En particulier, cette définition permet de munir d’une structure d’e.v.s. l’espace vectoriel E des applications linéaires de E dans son corps de base qui sont continues pour les suites.

On retrouve dans le cadre des e.v.s. l’importante notion de transposée d’une application linéaire (cf. algèbre LINÉAIRE ET MULTILINÉAIRE). Soit, en effet, E et F deux e.v.s., et u un morphisme de E dans F; désignons par E et F , comme ci-dessus, les e.v.s. des applications linéaires respectivement de E et F dans le corps de base (formes linéaires sur E et F), qui sont séquentiellement continues. Pour toute forme linéaire f 捻 F , la forme g = f 獵 u est une forme linéaire séquentiellement continue sur E, donc est un élément de E , et on vérifie facilement que l’application linéaire ^t u : F E , qui à f 捻 F fait correspondre f 獵 u 捻 E , est séquentiellement continue; on définit ainsi le morphisme ^t u transposé de u .

2. Définition des distributions

Il est clair que, pour généraliser la notion de fonction, il faut abandonner certaines propriétés usuelles des fonctions (par exemple le fait qu’une fonction prend une valeur déterminée en chaque point) pour ne conserver que certaines propriétés. L. Schwartz utilise comme notion essentielle la propriété d’opérer linéairement sur des classes de fonctions très régulières.

Méthode générale de construction

La méthode générale pour définir un espace de fonctions généralisées sur un ouvert 行 de Rⁿ est la suivante. On prend tout d’abord un e.v.s. 淪 de fonctions «suffisamment régulières» dans 行; par définition, l’espace des fonctions généralisées sur 行 est alors l’espace 淪 des formes linéaires séquentiellement continues sur 淪. Pour justifier la terminologie de «fonctions généralisées», il faut identifier les fonctions «régulières» sur 行 à des éléments de 淪 ; pour cela, on identifie une telle fonction f à la forme linéaire sur 淪:

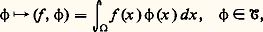où x = (x ¹, ..., x ⁿ ) et dx = dx ¹ dx ² ... dx ⁿ . Nous allons préciser ces indications générales en construisant en détail les distributions proprement dites.

Définition des distributions

On prend ici pour espace 淪 l’e.v.s. 阮( 行), défini ci-dessus, des fonctions indéfiniment différentiables et à support compact dans 行. L’espace 阮 ( 行) des distributions dans 行 est alors par définition l’ensemble des formes linéaires T séquentiellement continues sur 阮; on note indifféremment:

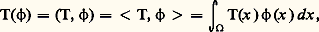la valeur de la distribution T (forme linéaire sur 阮( 行)) sur la fonction 﨏 捻 阮( 行). Remarquons que la dernière écriture est abusive; elle est utilisée car elle rappelle que, si T est une fonction, l’expression de T( 﨏) est donnée par une intégrale. Précisons ce point.

Si f est une fonction intégrable (au sens de la théorie de Lebesgue) sur tout compact de 行 (on dit alors que f est localement intégrable), on peut l’identifier à la distribution:

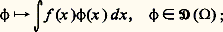les distributions définies par deux fonctions f et g localement intégrables dans 行 coïncident si et seulement si f et g «coïncident» au sens de la théorie de Lebesgue, c’est-à-dire sont égales presque partout ; ainsi, les distributions ne généralisent pas à proprement parler les fonctions, mais les classes de fonctions égales presque partout: si on modifie une fonction en changeant sa valeur en un point, par exemple, elle définit toujours la même distribution; on a bien abandonné la propriété des fonctions d’être définies par leur valeur en tout point.

La notion d’e.v.s. permet de définir la notion de suites convergentes de distributions : si ¹, ², ..., Tⁿ , ... est une suite de distributions, on dit, en accord avec la définition de l’e.v.s. 阮 ( 行), que cette suite tend vers une distribution T si:

pour toute fonction 﨏 捻 阮( 行). On peut montrer que, si pour toute fonction 﨏 捻 阮( 行) la suite de nombres complexes Tⁿ ( 﨏) tend vers une limite, l’application définie dans 阮( 行) qui à 﨏 捻 阮( 行) fait correspondre cette limite est une distribution, limite de la suite des distributions Tⁿ . Cette propriété est généralement très facile à vérifier et permet de définir de nombreuses distributions nouvelles à partir de distributions déjà connues.

La notion de suite convergente de distributions permet en particulier de définir les séries convergentes de distributions. Si (Tⁿ ) est une suite de distributions, on dit que la série de terme général Tⁿ est convergente (au sens des distributions) de somme T si la suite des sommes partielles est convergente au sens indiqué ci-dessus; on écrit alors Tⁿ = T.

Exemples

a ) Soit a un point de Rⁿ ; l’application qui à toute fonction 﨏 捻 阮(Rⁿ ) fait correspondre la valeur 﨏(a ) de la fonction 﨏 en a est une distribution appelée distribution de Dirac et notée 嗀^a . Ainsi, avec l’abus d’écriture signalé ci-dessus, on a: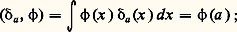

cette distribution permet de donner une définition mathématique rigoureuse de la «fonction» de Dirac mentionnée plus haut.

b ) On vérifie facilement que la fonction a définie sur R par

est une fonction indéfiniment dérivable, nulle par définition en dehors de l’intervalle [ 漣 1, 1]. Si on pose:

la fonction 福¹(x ) = a (x )/k appartient donc à 阮(R) et est d’intégrale égale à 1. Plus généralement, la fonction: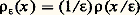

appartient aussi à 阮(R) et est d’intégrale égale à 1; d’autre part, 福 size=1^﨎 est nulle en dehors de l’intervalle [ 漣 﨎, 﨎] (fig. 1). Comme

pour toute fonction continue 﨏, il en résulte que, pour toute suite 﨎ⁿ tendant vers 0, la suite des distributions 福 size=1^﨎n (ou, pour être précis, la suite des distributions Tⁿ définies par ces fonctions) tend vers la distribution de Dirac au point O.

c ) Dans le plan, identifié à R², de la variable complexe z , on montre que la fonction f (x + iy ) = 1/ 神 z est intégrable sur tout compact; par suite, cette fonction définit une distribution, notée 1/ 神 z , qui, à toute fonction 﨏 捻 阮(R²), associe: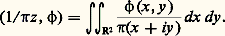

d ) Soit maintenant R³ l’espace de la géométrie élémentaire dans l’espace. La fonction x 料 1/(4 神 瑩x 瑩) est localement intégrable dans R³ et définit donc une distribution, notée 1/(4 神 瑩x 瑩).

e ) On peut montrer que, pour toute fonction 﨏 捻 阮(R), et pour toute suite 﨎ⁿ tendant vers 0, la suite des nombres réels:

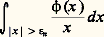tend vers une limite, indépendante de la suite ( 﨎ⁿ ) choisie, et que l’application qui à 﨏 fait correspondre la limite correspondante est une distribution, notée v.p.(1/x ), valeur principale de Cauchy; ainsi:

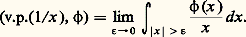Dans l’étude des équations aux dérivées partielles, Hadamard a été conduit à généraliser cette notion (distributions «parties finies»).

3. Propriétés des distributions

À partir d’une application linéaire séquentiellement continue L de 阮 dans 阮 (opérateur dans 阮), on peut définir, par transposition, un opérateur linéaire L dans l’espace 阮 des distributions:

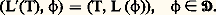Dérivation des distributions

Les distributions étant une généralisation de la notion de fonction régulière, essayons d’étendre aux distributions la notion de dérivation . Pour cela, analysons tout d’abord les propriétés des opérateurs de dérivation partielle pour les fonctions continûment dérivables dans un ouvert 行 de Rⁿ .

Pour toute fonction 﨏 捻 阮( 行), on a, si T désigne à la fois une fonction continûment dérivable dans Rⁿ et la distribution qu’elle définit:

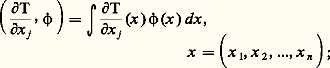mettant en évidence la variable x ^j , on peut écrire (en permutant les variables) x = (x , x ^j ), d’où dx = dx dx ^j , ce qui donne, par intégration par parties,

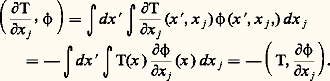Or, l’opérateur L = 漣 (face=F0019 煉/ 煉x ^j ) est séquentiellement continu dans 阮( 行) (cf. supra , Morphismes ); l’opérateur transposé, noté 煉/ 煉x ^j est donc un opérateur séquentiellement continu de 阮 ( 行) qui prolonge la dérivation au sens usuel. Pour toute fonction 﨏 de 阮( 行), la j -ième dérivée partielle de la distribution T donne donc par définition :

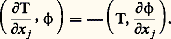Ainsi, par exemple, la distribution dérivée de la distribution de Dirac en 見 sur la droite est telle que ( 嗀 size=1^見, 﨏) = 漣 﨏 ( 見).

Support

Si 行 est un ouvert contenu dans 行, on a un morphisme naturel

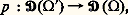qui à toute fonction 﨏 捻 阮( 行 ) associe la fonction p ( 﨏) obtenue en prolongeant 﨏 par 0 en dehors de 行 . L’opérateur transposé de p est l’opérateur p sur les distributions défini par:

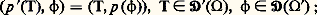p (T) est généralement noté T size=1^行 size=1, restriction de la distribution T à l’ouvert 行 . On dit que T est nulle sur 行 si T size=1^行 size=1 = 0.

Si T est une distribution dans un ouvert 行, on appelle support de T le complémentaire dans 行 de la réunion des ouverts 行 sur lesquels T est nulle. Par exemple, le support de la distribution de Dirac au point a de Rⁿ est constitué du seul point a .

Produit direct

Soit 行 un ouvert de l’espace Rⁿ de la variable x , et 行 un ouvert de l’espace R^p de la variable y , respectivement. Si T et U sont des fonctions continues dans 行 et 行 respectivement, la distribution T 憐 U dans 行 憐 行 définie par la fonction T(x ) U(y ) satisfait à:

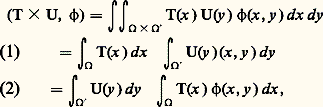pour toute fonction 﨏 捻 阮( 行 憐 行 ).

On peut montrer que lorsque T et U sont des distributions, si on considère les intégrales comme des accouplements distributions-fonctions (abus de notation signalé plus haut), alors les expressions (1) et (2) ont un sens, sont égales, et on peut montrer que l’application qui à 﨏 捻 阮( 行 憐 行 ) fait correspondre (1) ou (2) est une distribution. Cette distribution, notée T 憐 U, est appelée produit direct de T et U.

Convolution

Soit T et U deux fonctions continues et intégrables dans Rⁿ ; on appelle produit de convolution de T et U la fonction définie par la formule intégrale

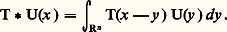La fonction T U ainsi définie est telle que, pour toute fonction 﨏 de 阮(Rⁿ ),

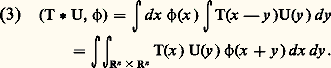On montre que, dans certains cas, on peut donner un sens à (3) pour des distributions T et U, et définir ainsi une distribution, notée T U. Cela est possible, par exemple, si l’une des distributions est à support compact. Sur R, on peut également définir le produit de convolution de deux distributions S et T qui s’annulent pour t 麗 0.

L’intérêt pratique de la convolution est que de nombreuses opérations usuelles sont des convolutions. Par exemple, pour toute distribution T sur Rⁿ et pour tout multi-indice 見:

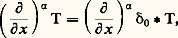où 嗀⁰ est la distribution de Dirac à l’origine des coordonnées. On voit l’intérêt de l’étude des équations de convolution , du type A X = B, où A et B sont des distributions connues; la résolution d’une telle équation est parfois appelée «déconvolution». Si A est une distribution à support compact, on appelle solution élémentaire de A toute distribution E telle que E A = A E = 嗀⁰; une solution élémentaire d’un opérateur différentiel

est alors par définition une solution élémentaire de la distribution A = P(face=F0019 煉/ 煉x ) 嗀⁰.

4. Séries et intégrales de Fourier

La plupart des grandes théories de l’analyse classique s’étendent aux distributions; nous nous limiterons ici à des indications rapides sur la théorie de Fourier (cf. analyse HARMONIQUE) en renvoyant à l’article calcul SYMBOLIQUE pour la transformation de Laplace.

Transformation de Fourier dans l’espace size=5崙

Le domaine naturel de la transformation de Fourier élémentaire est l’espace 崙 des fonctions indéfiniment dérivables à décroissance rapide ainsi que toutes leurs dérivées: c’est l’espace des applications 﨏 indéfiniment dérivables de Rⁿ dans le corps C des nombres complexes telles que: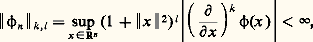

pour tout entier l et tout multi-indice k . Cet espace 崙(Rⁿ ) est une e.v.s. pour la notion suivante de suites convergentes: par définition, une suite ( 﨏ⁿ ) de fonctions de 崙 tend vers 0 si:

quels que soient l’entier l et le multi-indice k .

Pour 﨏 捻 崙(Rⁿ ), on appelle transformée de Fourier de 崙, la fonction: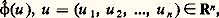

définie par la formule intégrale:

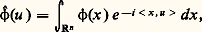où 麗 x, u 礪= u ¹x ¹ + u ²x ² + ... + u ⁿ x ⁿ désigne le produit scalaire dans Rⁿ . Cette définition de la transformation de Fourier n’est pas universelle; certains auteurs préfèrent prendre par exemple:

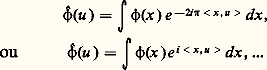On passe d’une définition à l’autre par un simple changement de variable dans l’intégrale définissant 﨏. Nous écrirons tout ce qui suit avec la convention indiquée, adoptée par de nombreux mathématiciens qui étudient les équations aux dérivées partielles. Dans l’article analyse HARMONIQUE, au contraire, on préférera adopter la seconde formule.

L’application 杻 qui à 﨏 fait correspondre sa transformée de Fourier 﨏 possède les principales propriétés suivantes:

a ) la fonction 﨏 est dans 崙 et

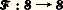est un isomorphisme de l’e.v.s. 崙 sur lui-même;

b ) pour tout couple de fonctions 﨏 et 祥 de 崙, on a les formules:

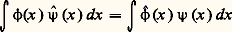(relation de Parseval),

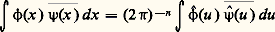(relation de Plancherel);

c ) l’isomorphisme réciproque de l’isomorphisme 杻 est défini par:

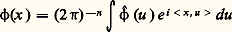(formule d’inversion de Fourier).

Transformation de Fourier dans size=5崙 size=5

On appelle distribution tempérée dans Rⁿ toute forme linéaire séquentiellement continue sur 崙; remarquons que, puisque l’application identique de 阮(Rⁿ ) dans 崙(Rⁿ ) est un morphisme et que toute 﨏 de 崙 est limite d’une suite d’éléments de 阮, la transposée de cette application identique est une injection. Cette injection fait apparaître l’espace 崙 des distributions tempérées comme un sous-espace vectoriel de l’espace vectoriel 阮 des distributions.

Par définition, on appelle alors transformée de Fourier d’une distribution tempérée T la distribution tempérée T définie par:

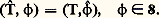Considérons par exemple la distribution sur R définie par la fonction x ; sa transformée de Fourier x est telle que:

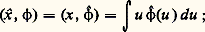un calcul facile montre que cette dernière intégrale vaut:

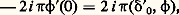où 嗀 ⁰ est la dérivée (au sens de distributions) de la distribution de Dirac en 0. Ainsi x = 2 i 神嗀 ⁰. Par des raisonnements analogues, on pourrait montrer que la distribution:

a pour transformée de Fourier: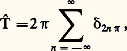

ce qui est équivalent à la relation de Poisson,

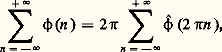valable pour toute fonction 﨏 捻 崙(R).

Coefficients de Fourier d’une distribution périodique

Comme d’habitude, on identifiera le tore T = R/2 神Z (quotient de R par la relation d’équivalence x 黎 y si x 漣 y est un multiple entier de 2 神) à la circonférence unité du plan complexe, tout point de cette circonférence étant caractérisé par son affixe e ⁱ size=1, ou, ce qui revient au même, par son abscisse curviligne . Cette identification établit une correspondance naturelle entre les fonctions définies sur le tore T et les fonctions périodiques de période 2 神 définies sur R. Par définition, on dit qu’une fonction définie sur T est indéfiniment dérivable s’il en est ainsi pour la fonction périodique associée; l’espace 阮(T) des fonctions indéfiniment dérivables sur T est alors muni d’une structure d’e.v.s. en convenant qu’une suite ( 﨏ⁿ ) tend vers 0 dans 阮(T) pour n秊, si (d /d )^k 﨏ⁿ tend uniformément vers 0 sur T, n秊, pour tout entier k .

Par définition, une distribution sur T est alors une forme linéaire séquentiellement continue sur 阮(T); il est facile de voir que l’espace 阮 (T) de ces distribution est en correspondance bijective avec l’ensemble des distributions périodiques sur R, c’est-à-dire les distributions T telles que:

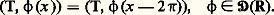En procédant comme ci-dessus, on peut définir des opérations dans 阮 (T): dérivation, produit direct, convolution, etc. Si f est une fonction intégrable définie sur T, elle définit la distribution:

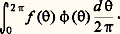Par définition, on appelle transformée de Fourier d’une fonction 﨏 捻 阮(T) la suite doublement infinie 﨏 = ( 﨏^k ) size=1^漣秊麗k size=1^麗秊 définie par:

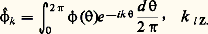Pour développer une théorie similaire à celle de la transformation de Fourier vue ci-dessus, on est conduit à introduire l’espace vectoriel s des suites doublement infinies à décroissance rapide, c’est-à-dire les suites

a = (a ^k )^k size=1^捻Z telles que:

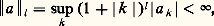pour tout entier l ; cet espace est un e.v.s. si on convient qu’une suite (a ⁽ⁿ⁾ ) d’éléments de s tend vers 0 si pour tout entier l la suite 瑩a ⁽ⁿ⁾ 瑩^l tend vers 0 pour n秊.

On montre alors que l’application 杻 définie par 杻( 﨏) = 﨏 est un isomorphisme de 阮(T) sur l’espace s , l’application inverse faisant correspondre à la suite a = (a ⁿ ) la somme de la série de Fourier:

La relation de Plancherel prend ici la forme: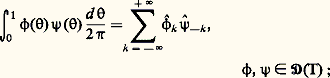

elle montre que la transposée de 杻^-1 est un isomorphisme de 阮 (T) sur s qui prolonge 杻. Si on note encore 杻 cette application transposée T 料 T, on a:

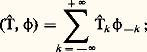en particulier, si on fait 﨏( ) = e 漣ik , on obtient:

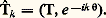On peut caractériser l’espace s des transformées de Fourier des distributions tempérées; c’est l’ensemble des suites T = (T^k ) à croissance lente , c’est-à-dire pour lesquelles il existe un entier l (dépendant de T) tel que T^k /k ^l reste borné pour |k |秊.

Une application

Les distributions peuvent servir à étudier le comportement des fonctions analytiques; voici un exemple simple d’une telle situation.

À une distribution T sur le tore, associons le couple 淪 = ( 淪⁺, 淪^-) des deux fonctions holomorphes ainsi définies:

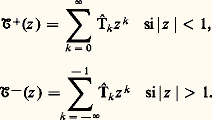Soit maintenant P( ) un polynôme trigonométrique, c’est-à-dire une combinaison linéaire finie d’exponentielle e ^ik size=1:

on peut écrire aussi, par abus de notation: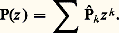

Soit C⁺ et C^- deux circonférences de centre 0 et de rayons 麗 1 et 礪 1, orientées dans le sens rétrograde et dans le sens trigonométrique respectivement. Développant 淪 et P en série, on obtient (fig. 2):

donc: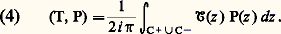

Pour 0 麗 r 麗 1, posons maintenant:

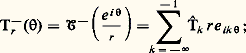ainsi, on a: T^{r +} 漣 T^{r -} = P^r T,

est le noyau de Poisson. On peut voir que P^r tend vers 嗀⁰ dans 阮 (T) pour r1; il en résulte que l’on a dans 阮 (T):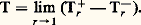

On interprète le résultat précédent en disant que la distribution T est la différence des valeurs au bord (le long de la circonférence unité) des fonctions holomorphes 淪⁺ et 淪^-. Par exemple, considérons:

Développant 淪 en série entière (en z ou en 1/z ), on voit que à 淪 est associée une distribution ^N dont les coefficients de Fourier sont: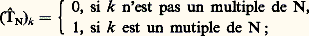

la formule (4) ci-dessus montre alors que pour tout polynôme trigonométrique P:

Si 嗀^{j N} désigne la mesure de Dirac sur T concentrée au point z ^{j N}, on a donc:

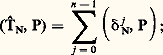comme toute fonction de 阮(T) est approchable uniformément par une suite de polynômes trigonométriques, on en déduit que ^N est la somme de la série:

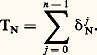De manière générale, toute suite doublement infinie (â ^k )^k size=1^捻Z, à croissance lente (cf. supra , Coefficients de Fourier d’une distribution périodique ), est la suite des coefficients de Fourier d’une distribution A sur T, ce qu’on écrit symboliquement :

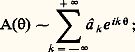de plus, A est la limite dans 阮 (T) des distributions définies par les polynômes trigonométriques:

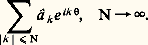Autrement dit, la série de Fourier d’une distribution converge vers cette distribution dans 阮 (T); mais bien entendu cela n’entraîne pas que les sommes partielles convergent pour tout .

Encyclopédie Universelle. 2012.